調和(倍音)の法則、その最も基本的な原則は、ある構造全体を2分の1、3分の1、5分の1・・・と次々に厳密に整数分割していく(整数比を厳守する)、というものである。その「全体(whole)」そのものは「基本周波数(the fundamental)」あるいは「第1倍音(first harmonic)」と呼ばれる。その基本構造(全体)をきれいに「半分に折りたたむ」と、2等分された (つまり基本周波数を2分割した) ことになる。この半分になった部分が「第2倍音(second harmonic)」である。2つではなく、3つに折りたたむと、3等分したことになる。これが「第3倍音(third harmonic)」である。この「調和(倍音)数列(harmonic progression)」、つまり基本構造と整数分割された各部分という関係は、人間についても同じことが言える。
思考やできごとから、明確な物体、そしてその周囲の環境にいたるまで、
多様体構造であればどんなものであれ、分析分解して、その調和成分(「パーシャル」という呼ぶほうが好きだが)によって完全に表現することが可能である。そのパーシャルひとつひとつは、構造体の全体を整数分割した部分に備わる、固有の性質や独特のふるまいという以外の何物でない。したがって、このようなパーシャルをひとつにまとめれば、それだけで、表現するものを完璧に再構成することができるのである。
知覚という感覚装置を使って、ひとや物体、ものごとを観察するとき、私達は実にすばやく、「これは膨大な数の異質な成分からなる配列だ。異質な成分同士が互いに織物の糸のように絡み合って、今見ている対象の形や動きを創り出し、目に見えるものにしているのだ」と結論を出す。けれどもこれまでは、観察対象《その人や物、できごと》を構成している要素が多種多様で、その数があまりに多いため、一度にうまく処理することができなかった。そのため、変容を目的として相互に作用(interact)するはおろか、対象を理解することことすらできなかった。
けれどもここで、その対象を「パーシャルという形」で捉えるなら、
従来の方法では得られなかったユニークな視点を得ることができる。多様な要素が複雑に交錯した状態を扱うのではなく、パーシャルとして表現された、それ自体は均質な「全体」としてのひとに働きかけるのである。つまり、果てしなく変化し続ける対象の多様性を、一様なパーシャルのコヒーレントな集合にまで凝縮して、つまり多くのものをひとつ(Oneness)に統一して、見るわけである。これによって、対象の多様体構成と動き(力学)を同時に観察するだけでなく、単一の統合された全体としての対象に変化を及ぼすことができるようになる。
この「再統合」を成し遂げるには、調和の法則に忠実に従うことが極めて重要となる。もし、その対象のパーシャルを、全体の整数比という形で収集することができなければ、そこから再現されるもの、及び、その結果としての変容は不完全で、ばらばらに分裂したものになるだろう。厳密に整数比のパーシャルを収集し、再分配することで、確実に「パズルの断片」の正しい番号《位置》が判るだけでなく、それぞれの断片がすきまなく、あるべき場所にぴったりと完璧に納まるようにすることができるのである。
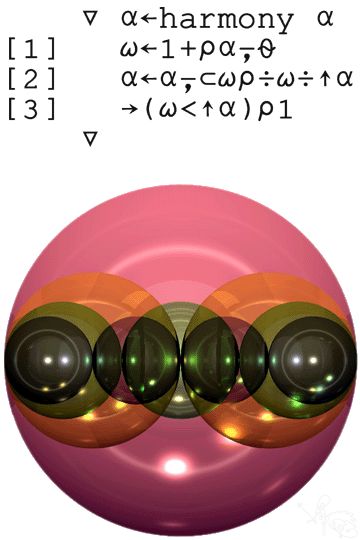
冒頭及び下の画像「調和/ハーモニーの表現」図に示されているのは、
全体(基本周波数・第一倍音)から第4倍音までの構造である。色分けされた球はそれぞれパーシャルを表している。2分割、3分割、4分割され、それぞれ各部が連続したセットになっているが、そのセットはどれも、全体の内部に、重なっているところも隙間もなく、きっちりと収まっている。まさしくここに、調和(倍音)の法則の本質がはっきりと表現されている。
ここでもうひとつ、取上げなければならない要素がある。「オリジン(源 Origin)」である。調和級数《連続倍音》を基本周波数の整数比分割(基本周波数を1/1として、1/2、1/3、1/4)であると考えるとき、全体の基本周波数より前に存在する要素がもうひとつある。連続倍音のなかにあって、数学的不可能性を構成する、すなわち、従来は「定義不能」とされてきた値(1/0)である。しかし、これは私達人間を現す公式において極めて重要な成分である。オリジンは、私達の対象(課題)とその環境との関係と同時に、その根源(原因 Source)との関係 (すなわち、「あらゆるものの基本的な相互連結」) を統合し包含する。

