・ 調和の法則は、現実を支配する何らかの規則が存在することを示唆しています。その基礎となっているのは、｢最初の原因（First Cause）｣、すなわち宇宙万物一体（The Universal One）の原理です。この根源における和合（Unity at the Origin）なしには、歴史や運命の調和もありえません。
・ 調和の法則の、最も基本的で重要な要素は、元となる完全体構造の連続的整数分割を堅持することにあります。その｢完全体（whole）｣の全体は、「基音(基本周波数)」あるいは｢第1倍音｣と考えられます。その元の構造物をきれいに｢半分に折りたたむ｣と、均等なふたつの部分ができます（つまり、基本の振動源の長さが2分割されたということです）。この半分の長さの振動数は元の2倍で、これを｢第2倍音｣といいます。半分でなく3等分した場合は｢第3倍音｣になります。この｢倍音進行（harmonic progression）｣は、私達人間の基本構造の整数分割にも当てはまります。
多種多様な構造体はみな、
想念あるいは出来事から意識する対象、およびそれを取り巻く環境まですべて、それ自身の倍音成分(｢パーシャル｣と呼ばれています)によって、破壊されることもあれば、充分に表現されることもあります。その個々のパーシャルはどれも、元の全体構造を整数分割したものの特有の性質や反応にほかなりません。このような倍音成分(パーシャル)をまとめるだけで、その成分が表現するものを完璧に再現することができるのです。
自分の知覚という感覚手段を用いて、
対象あるいは出来事を観察するとき、私達は、それが膨大なデータの配列から形成されていると、即座に推断します。その互いに異質な部分から構成された配列が、互いに密接に関わりながら、観察対象の形態と同時に力学/変化のあり方をも表しているのです。けれども対象があまりにもたくさんの異なる要素の集合であることと、従来の型にはまった方法では、そのすべてを同時に効果的に処理することができないために、私達は、変容するために対象を理解することはおろか、充分な相互作用を持つことさえできなくなってしまうのです。
けれども当社では、
感知する対象の｢パーシャルの形｣に注目するうちに、従来の方法では到底得られなかったような、ユニークなアイデアを得ることができました。多様な要素の複雑な相互作用を扱うのではなく、複数のパーシャルに、共通して現れる｢全体｣の表出を扱うのです。こうすれば、私達が出会う、多種多様なものごとの果てしない流れも、一様なパーシャルからなる、ひとつの整然とした集合という形で見ることができます。多くのものをひとつなものに収束するわけです。この結果、いくつもの異質な要素から構成された対象とその力学/変化を、すべて同時に観察できるだけでなく、その対象自体を、ひとつの統合された全体と見なして、そこに変化を及ぼすこともできるようになったのです。
調和の法則の規則に忠実であることは、
この｢再統合（re-synthesis）｣の成否を握る重要なポイントです。もしも、対象の全パーシャルが全体(基本周波数)の整数比に収束されていなければ、その現れも、またその結果得られる変容も不完全で、ばらばらになります。パーシャルを集め、それを厳密な整数比で再分配することで、｢ジグソーパズルの断片｣にそれぞれ適切な番号をつけて整理できるだけでなく、その個々の断片を、他の部分と隙間なくぴったり合うような完璧な位置に収めることもできるのです。
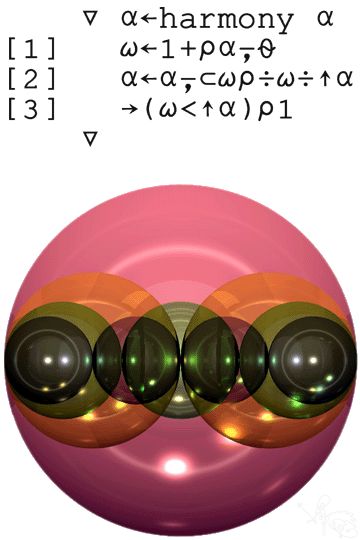
図-Algorithm and Graphic of Harmonic Lawは、それぞれのパーシャルを色違いの透明な球体として現し、第1倍音(基音)から第4倍音までの調和(倍音)列を表現したものです。各倍音(訳注＝同じ大きさの球)のセットは2個組(第2倍音)であれ、3個組(第3倍音)であれ、それぞれが全体のなかに隙間なくぴったりと納まっています。ここにはまさに、調和の法則のエッセンスが正しく的確に表現されています。
・ もうひとつ、ここで言及しなければならない成分要素があります。｢根源（Origin）｣です。倍音列を基本周波数の整数分割比(基本周波数を1/1としたとき、第2が１/2、第3が1/3､､､)であると考えるとき、そこにはもうひとつ、全体の基本周波数に先だって存在する成分要素があります。倍音列のなかに置くと、数学的な不可能性を生じさせるこの要素は、これまで一般的には｢定義されない（un-definable）｣値(1/0)とされてきましたが、当社の考え方においては、最も重要な構成要素となっています。この根源は、ものごととその源との関係と同時に、ものごととその環境との関係(すなわち、あらゆるものとの基本的相互連結)をも端的に表現しています。根源はスペクトルに現れることはありませんが、その内部に、ビッグバンの最初の瞬間から存在しているのです。
ハーモニー(和声/調和)のなかには、必ず多種多様な部分が相関しつつ存在しますが、
重要なのは、それが｢調和した多様性｣つまり、統合された全体を基本とする部分同士の関係であるということです。この法則は、オクターブの法則という名でも知られています。相関する各部の関係、すなわち性質の統一（unity of quality）の規則を定義すると同時に、その成長と発展の間にいくつの段階があるか、つまり全体がいくつのパートから構成されているかを明らかにするものです。これは社会の調和の鍵となるものです。多様なものが調和していなければなりませんから。
《訳注=オクターブの法則：音楽、化学、神秘学等多くの分野で用いられる基本法則のひとつ。音楽、振動学においては、基本振動数の2倍の振動数は1オクターブ上の音であり、その間が八つの音に分けられることを指す》
・ ハーモニーには、各部分間の的確な時間的空間的間隔がふくまれています。これは、人為的な時間と世界標準時（universal time）の間に起こりうる差も示唆しています。
・ ハーモニーは、純粋なエッセンスから成り立っています。多くの信念体系は、調和が確立されるまで、浄化（純粋化）の必要について堂々巡りを繰り返します。
・ ハーモニーには、和音(調和)と不協和音(不調和)という二元性がふくまれており、これらふたつの一見相反するものを近づけ、その相違を解決するためには、何らかの力あるいはエネルギーが必要となります。私達はこの概念を、トリユニティ(三統合Triunity)と呼んでいます。トリユニティによって、潜在しているものが確実に調和した状態で現れるようになるのです。
・ ハーモニー（和音の連結）と不協和音についてはどちらが良いかとか、正しいとか、誤っているとかいうことはありません。けれども、連続的（continuous）なものとトランジェント（transient/過渡的一時的）なものという二元性の概念はあります。このふたつは相補関係にある一対というわけではなく、対称(バランス)関係にもありません。このふたつの関係は、不協和音が和音の進行に不連続性を持ち込む際に起こる対立、葛藤を表現しているのです。例えば、反抗（Rebellion）というのは侵略的なトランジェント(過渡特性)の一例ですが、一方、調和(ハーモニー)というのは連続的な機能です。位相空間では、そのふたつの相違が明らかになります。これを音響学的に説明するよい例があります。穏やかに流れ落ちる滝の音と、銃声のスペクトルを分析してみると、どちらのスペクトル分布も、音の大きさ(マグニチュード)は同じですが、銃声の方は、全パーシャルが位相空間内の一点に集中しているのです。このような位相の強制的集束によって、トランジェントが生まれるのです。一方、連続的なまとまりを持ったパーシャルの場合は、具現化サイクルの中いっぱいに分布域が広がります。
《訳注＝過渡特性：波形の最高値から最小値へ、あるいはその逆へと変化する瞬間。非常に大きなエネルギーを持ち、音のキレを左右する》